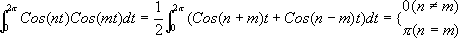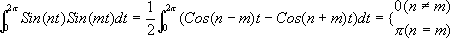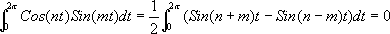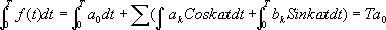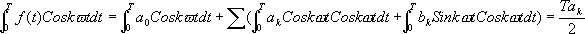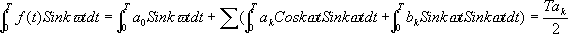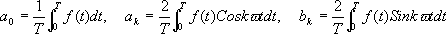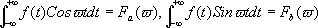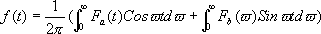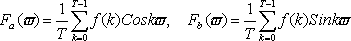[an error occurred while processing this directive]
[an error occurred while processing this directive]
フーリエ解析
フーリエ解析で何が出来る?
フーリエ解析は、元々は微分方程式を解くために生まれました。しかし、現在では音や画像といった「マルチメディア」に関する分野で不可欠になっています。また、整数論の分野でも重要で、最近有名になった量子コンピュータで暗号解読が出来る「Shorのアルゴリズム」でも重要な位置を占めています。
このフーリエ解析、基本的な発想はすごく単純です。一言で言えば、「あらゆる波を Sin の和で表す」というものです。計算も、Sin/Cosと微分・積分を知っていれば十分理解可能です。ここでは、複素関数の知識は使わず、高校生でも理解できるポイントをまとめてみました。
(きぃたんさんにアドバイスいただいて、少し説明修正しました)
音は時間の関数
音って何でしょう。「何」といわれても困るかもしれませんが、音とは「空気を伝わる波」です。そして、波は「空気の震えてる度合い(振幅)」として数字で表すことが出来ます。この数字を電流としてスピーカーに流すと、音を再現することが出来ます。これが私たちが聞いているCDやパソコンの音楽の仕組みです。
これをもう少し数学的に考えてみましょう。
音のデータは時間が決まると値が定まるのだから、時間の関数f(t)と書くことが出来ます。二つの音を加えるのはf(t)+g(t)。カセットテープを二倍の早回しするのはf(2t)。あなたがCDを買うのは{f(t)|0(分)<t<74(分)}という関数を買っているのです。実感湧きますか?
音の三要素
音、といっても色々あります。話し声、音楽、水が流れる音、車のエンジン音、ジェット機の爆音などすべて音です。では、一番基本的な音は何でしょう。先に述べた通り音は波ですから、ここは一番基本的な波、Sin波を考えるのが自然でしょう。Sin波を音として聴くと、音叉の音が一番近いようです。
Sin波では、音の「高さ」「大きさ」を簡単に考えることができます。Sin波は周波数ωと振幅Aを用いてf(t)=A*sin(ωt-t0)と書くことができますが、ここでωが音の高さを表し、Aが音の大きさを表します。例えば,一般に音叉は「ラ」の音で、これは440Hzなのでf(t)=A*sin(440*t/(2π)-t0)と表すことができます。なお、振幅Aは叩いた強さや観測する場所によって変わります。
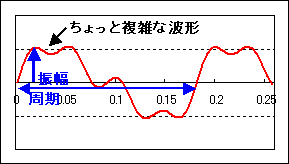
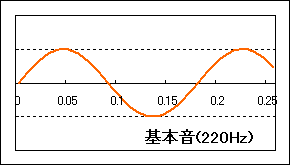
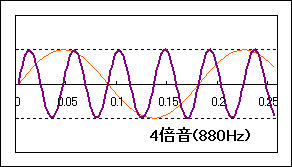
では、Sin波以外の音では「高さ」「大きさ」はどうなるのでしょうか?Sin波以外ちょっと複雑な波形でも、周期Tがあれば、この逆数から周波数を求めることができます。このとき、一周期の波形が音の音色を決めています。音の大きさも振幅で大体決めることができます。ここで出てきた「高さ」「大きさ」「音色」を、音の三要素と言います。(下図参照)
音の足し合わせ(和音)
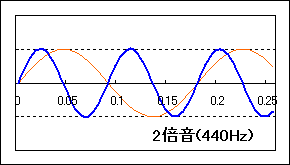
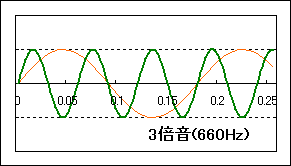
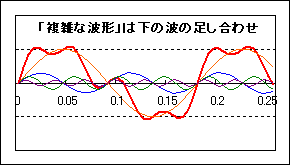
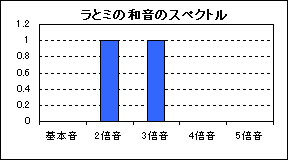
先程も述べましたが、二つの音が同時に鳴っている状態を表すには,単に二つの式を足すだけでOKです。例えば、ラ(440Hz)とミ(660Hz)の和音なら、下の図のようになります。
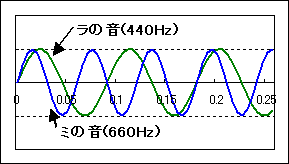
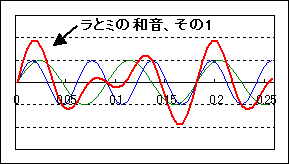
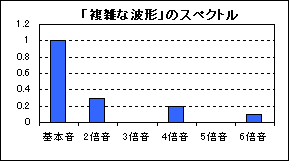
しかし、こうして波を足すと、もはや初めの「音の三要素」が見えなくなってしまいました。代わりに見えるのは、複雑な波形を持った一つの音です。この音の周波数は220Hzで、元の音のどちらとも一致しません。これは新しい音色の音なのでしょうか、それとも和音なのでしょうか?実際にこの音を聞いてみると、聴きようによっては一つの音にも和音にも聞こえます。
このように、先の「音の三要素」の説明だと、複数の音が鳴っている場合、波形を見ただけでは鳴っている音の数を判断できないため、音色と複数の音の和を区別することができません。
さらに、問題な事には、二つの音を足すタイミングをちょっとだけずらしてやると、様々な波形の音が出来てしまいます。例えば、先のラとミの和音なら、下のような波形も考えることが出来ます。
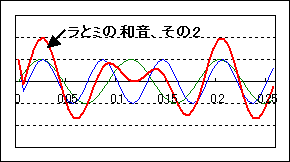
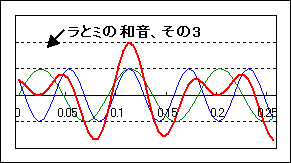
これらは聴くと同じに聴こえますが、波形はずいぶん違っています。二つの音を足すタイミングは無限に存在するので、こうした同じ音を表す波形も無限に存在することになり、分析にはとても不便です。
「フーリエ展開」
フーリエ展開の計算
先程は「これはこうなる」という形でフーリエ展開の実例を挙げましたが、実はこうした展開は計算で簡単に求めることができます。ここでは、その計算法を挙げてみます。
音の関数をf(t)と書くと、これがSin波の和で表せる、というのは、
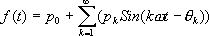
と書けます。ここで、p
0は直流成分、p
kは各Sin波の強さを、θ
kは各Sin波をずらして足してもいいことを表しています。ここで、計算の都合上θをばらしてみます。加法定理より
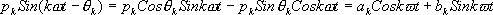
となるため、このa
k,b
kを用いて先の式を書き直すと
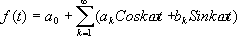
となります。
さて、いよいよ各フーリエ係数を求めてみます。その前に、ちょっとした積分の復習を。SinやCosを一周期で積分すると0ですが、SinやCos同士を掛けて積分すると、以下のようになります。
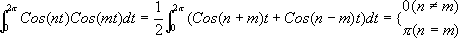
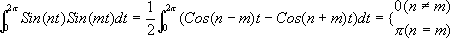
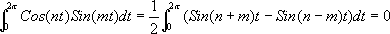
これを見ると、Sin波二つを掛けて積分すると、位相と周波数がそろっているときに限り値が0でないことがわかります。これを使うと、先のak、bkを求めることができます。
まず、音をそのまま積分してみます。
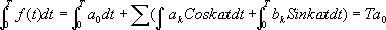
SinやCosの成分は消え去って、a
0が求まりました。次に、Cosを掛けて積分してみます。
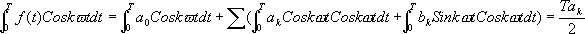
次はa
kが求まりました。最後に、Sinを掛けて積分すると
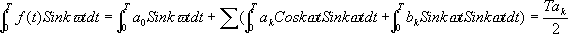
と、見事b
kが求まりました。
各成分ごとの強さ…という意味でc
kの表示に戻したいときは、先の
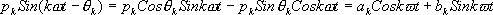
から導かれる関係、
c
k2=a
k2+b
k2
を使って求められます。
まとめてみると、以下のような積分でa
k、b
kを求めることができます。
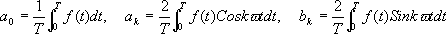
周期がない/分からない音→「フーリエ変換」
これで、周期がある音については周波数ごとの分析ができるようになりました。この基本音ごとの強さを見れば、どんな音かほぼ推定することができます。しかし、周期がない、あるいはまだ周期が分かっていない音ではどうでしょうか?周期が無い音など分析しても無意味だ、と思われるかもしれませんが、実際の声や音はむしろ周波数がはっきりしているほうが稀です。
このような場合も、ちょっと工夫することで「どの周波数成分がどれだけ含まれているか」を計算することができます。その工夫とは、音の周期を無限大と考えることです。周期を無限大と考えると、先の「基本音」「n倍音」は全ての周波数の正弦波を表すことになり、スペクトルは連続になります。しかし、そのままT→∞にするとスペクトルの強さは1/Tに比例するので→0になってしまいます。そこで、これは(T/π)倍したものを用いることにします。これにより、周期が分からない音も、周波数別の強さが分かることになります。これを「フーリエ変換」と呼び、一般的な音の解析に多用されています。
ただし、後の計算を見てもらえればわかるのですが、フーリエ変換をするにはちょっとした条件が必要になります。それは、t→±∞の時にf(t)→0となることです。とはいえ、実際の音を扱う限りは信号長は有限なので、これが問題になることはそうありません。
フーリエ変換の計算
さて、実際の計算です。ここでは直流成分(a
0が無い信号を仮定します。
フーリエ展開の時の変数は、元周期の何倍音かを示すkだったわけですが、周期を無限大にした場合は基準音がないので、単純に周波数そのものを変数に取ることにします。また、先程も述べたとおり、フーリエ係数自体は(T/2π)倍したものをそうすると、先のa
kやb
kを求める式はもっと簡単になって、
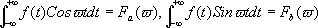
となります。ここ、さっきT倍ではなくて(T/π)倍したのが効いています。こうして出てきた値は、「周波数ωの強さはF(ω)」であることを示しています。この「強さ」という言葉は、フーリエ展開のときみたいに、各周波数成分をその強さで足していったら元の音になる…というわけではありません。ことフーリエ変換された関数F(ω)からもとの音を再現するには、
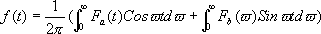
とします。
波形をデジタルにする…サンプリング
フーリエ変換は、実際の音声や画像のデータに用いてこそ真価が発揮されます。その計算はパソコンを用いて行うのですが、パソコンで扱うデータはデジタルでなければなりません。このアナログデータをデジタルに変換する処理をサンプリングといいます。
といってもそんなにすごい処理をするわけではなく、下図のように、「サンプリング周波数」に応じてデータを間引きして、そこの値を記録していけばいいわけです。サンプリング周波数は高いほうが正確できれいなデータを記録できますが、その分データのサイズは大きくなります。
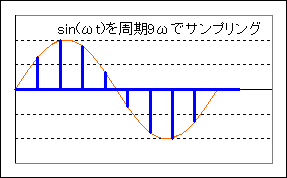
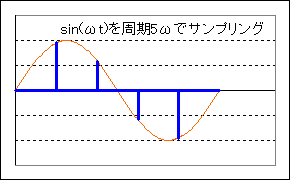
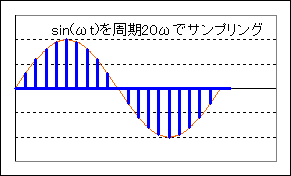
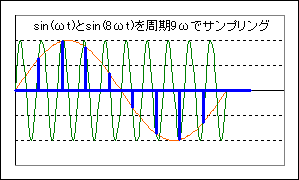
ところで、最後の図を見て下さい。これはSin(ωt)を周期9ωtでサンプリングしたものなのですが、これはSin(8ωt)をサンプリングした物とまったく同じで区別がつきません。つまり、あまりにもサンプリングが荒いと、正確なデータとはなりません。これについては「サンプリング定理」というものが知られていて、「ωHzの音を正確に記録するには、最低2ωHzでサンプリングする必要がある」というものです。つまり、パソコンでの計算では何Hzまでが意味のある計算なのかを常に意識する必要があります。
離散フーリエ変換
さて、パソコンでフーリエ変換をすることを考えてみます。とはいえ、先程説明したような無限大の計算なんてとても出来ないので、「データがあるところまで」計算したらいいです。また、積分という操作は、無限に足すという和の操作に置き換えます。また、パソコンで扱うときは波形はデジタルにしないといけないのですが、このとき先の「サンプリング定理」により、考える周波数はサンプリング周波数/2までにします。
これを式で表すと、
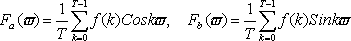
となります。ただし、Tはデータの数、ωはサンプリング周波数/2までの範囲で考えることにします。データ個数が有限なので、フーリエ変換の時とは違って「データ個数で割る」という操作が復活しています。(このあたりは定義の問題で、本質的じゃないです)
この離散フーリエ変換が、一般にマルチメディアデータを扱う際の一番の基本になっています。





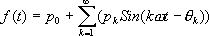 と書けます。ここで、p0は直流成分、pkは各Sin波の強さを、θkは各Sin波をずらして足してもいいことを表しています。ここで、計算の都合上θをばらしてみます。加法定理より
と書けます。ここで、p0は直流成分、pkは各Sin波の強さを、θkは各Sin波をずらして足してもいいことを表しています。ここで、計算の都合上θをばらしてみます。加法定理より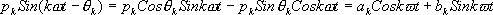
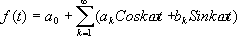 となります。
となります。