[an error occurred while processing this directive]
[an error occurred while processing this directive]
ガロア体と拡大体
集合と演算
CRC やリードソロモン符号の計算では、普通の足し算やかけ算とは少し違った、有限体と呼ばれる演算が用いられます。
これは、一般的な足し算やかけ算の意味を少し換えて、ビット演算と相性が良いようにしたものです。
演算…というと、普通は+、−、×、÷しか思いつきません。小学校から習ってきた数学は、この四種類を基本に構築されてきました。でも、世の中にはもっと色々な演算があることが知られています。
「演算」を抽象的に考えると、
- 「ある集合の中の二つの値から、一つの値を作る操作」
です。イメージ的にはこんな感じ。
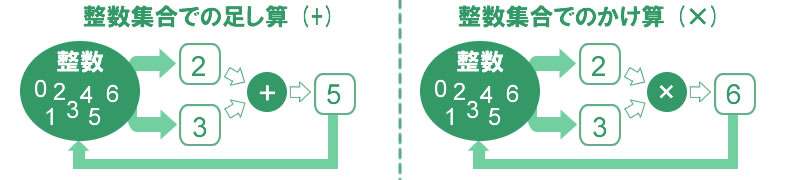
これは、整数集合での足し算を示しています。
元々の 2 と 3 は「整数」という集合の中身で、演算の結果の 5 や 6 も 整数集合に含まれます。
つまり、演算には、必ず対象とする集合があります。
小学校で初めに習う+、−、×、÷ が対象とする集合は整数です。その後、中学、高校と進むにつれ、色々な集合が導入されています。自然数や実数のほかにも、複素数 (1+i, 0, 2-3i, ...)、ベクトル ( (1,2), (0,3), ... )、行列などがあります。他にも、こんなのも集合です。
- 0, 1
- y = x + 1 を満たす (x, y) の集合
- x の多項式全体 (x, x2, 2x, x2 + x + 1, ...)
こういったものすべてに対し、演算を考えることができます。
演算というのは、先の定義によれば「集合の中の二つの値から、一つの値を得る操作」なので、相関表を作れば色々な演算が作れてしまいます。
普通の足し算の場合は、以下のような相関表が書けます。
| + | 0 | 1 | 2 | 3 | ... |
|---|
| 0 | 0 | 1 | 2 | 3 | ... |
|---|
| 1 | 1 | 2 | 3 | 4 | ... |
|---|
| 2 | 2 | 3 | 4 | 5 | ... |
|---|
| ... | ... | ... | ... | ... | ... |
|---|
この相関表を適当に作れば、色んな演算が作れます。下のようなものも、一応演算です。
| +(?) | 0 | 1 | 2 | 3 | ... |
|---|
| 0 | 0 | 1 | 8 | 3 | ... |
|---|
| 1 | 1 | 12 | 0 | 34 | ... |
|---|
| 2 | 21 | 3 | 8 | 5 | ... |
|---|
| ... | ... | ... | ... | ... | ... |
|---|
とはいえ、めちゃくちゃな集合、演算を考えることにあまり意味はありません。
CRC の場合に欲しいのは、「普通の演算でいう、割り算に近いけど、繰り下がりが起こらないもの」という演算です。
これを実現するために、上手な集合の定義、演算の定義をしてみます。
素数 P で割った余りの足し算、かけ算
まずは、繰り下がりがある、素数で割った余りを計算する演算を考えてみます。
余りを計算するには、まず割る素数 P が定義されています。
整数の集合には 0, 1, 2,... と無限の数がありますが、P で割った余りを計算することで、
あらゆる数は 0, 1, 2,... P-1 のどれかと同じ値になります。
つまり、整数という無限の元を持つ集合を、有限の集合に限定できたことになります。
この 「P の余り」の集合で + や × のような演算を考えると、それなりにうまく成り立っていることが分かります。
例えば、3 で割った「余り」の集合を考えてみます。
この集合では、あらゆる整数は {0, 1, 2} のいずれかに等しいことになります。
例えば、以下のような関係が成り立ちます。
また、足し算やかけ算の表は以下のように書けます。
この、素数 P で割った余りの足し算、かけ算は、いくつか都合の良い性質があります。
- 計算は有限の集合で定義されている
- +, ×に対し、結合法則 ( a + (b + c) = (a + b) + c, a × (b × c) = (a × b) × c ) が成り立つ
- 分配法則 (a + b) × c = a × c + b × c が成り立つ
- a + ? = b のとき、? に入る元がただ一つ定まる
- a * ? = b , a ≠ 0, b ≠ 0 のとき、? に入る元がただ一つ定まる
このような集合および演算 +, × をまとめて、
GF(P) と呼びます。
(GF はガロア体: Galois field の略) です。
上記の性質は、GF(P) が「体」であることから帰結される性質です。
この演算は、結果が必ず有限の範囲で定義されているため、数を通例限られたビット長で表すコンピュータでの処理には
都合がよいものです。また、その他の性質により、通常の演算で成り立つ概念をそのまま取り入れることができます。
(引き算、割り算、素因数分解、連立一次方程式、割り算など)
一方で、この演算には先ほど述べた繰り下がりの存在があったり、割る数が素数でないといけなかったり、という
制約があります。そこで、この「余りの演算」に似た演算を探してみます。
割り算ができるためには (CRC の条件)
集合 S 上での割り算について考えてみます。
以下の関係が成り立っているとします。
a / b = p ... q (ただし a, b, p, q ∈ S)
このとき、a, b, p, q には以下の関係が成り立っています。
a = b * p + q
b > q
これは、普通の×、+などについて割り算の定義を考えたものですが、×や+の定義を変えるときには、
上記を満たすような p, q がただ一種類に定まるとは限らなくなってしまいます。
普通の割り算のように、q がただ一種類に定まるためには
- 足し算ができて、かつその値が一通りに定まること
- かけ算ができて、かつ元が 0 でないとき、その値が一通りに定まること
などの条件が必要です。
こうした、演算と集合が満たす性質をまとめたのが、群や体といった、数学の一分野になっています。
体: ちゃんと余りが計算できる演算
ここでは、集合 S に対して扱いやすい+、×の性質として、体 (たい) を定義します。
この「体」の性質を満たしていれば、余りの計算はもちろん、リード・ソロモン符号化で用いる
連立一次方程式が解ける、など、演算としては申し分ない性質を持っていると言えます。
以下の説明は、Wikipedia の
体の記事からの引用です。
- K は加法に関してアーベル群である:
- a, b, c を K の任意の元とするとき、結合法則 a + (b + c) = (a + b) + c が成り立つ。
- a + 0K = 0K + a = a が K の元 a の取り方に依らずに満たされる零元と呼ばれる特別な元 0K が存在する。
- a が K の元ならばそれに対して a + (?a) = (?a) + a = 0K を満たす、マイナス元と呼ばれる元 ?a が常に存在する。
- 交換法則が成り立つ。つまり K のどんな元 a, b についても、 a + b = b + a となる。
- K は乗法に関してモノイドであって、0 以外の元が群をなす:
- a, b, c を K の任意の元とするとき、結合法則 a(bc) = (ab)c が成り立つ。
- a1K = 1Ka = a が K の零元 0K でない元 a の取り方に依らずに満たされる単位元と呼ばれる特別な元 1K が存在する。
- a が零元 0K でない K の元ならばそれに対して aa?1 = a?1a = 1K を満たす、逆元と呼ばれる元 a?1 が常に存在する。
- 乗法は加法に対して分配的である: a, b, c を K の任意の元とするとき、a(b + c) = ab + ac, (a + b)c = ac + bc が成り立つ。
上記は厳密な定義ですが、結局、以下の性質が成り立てば大体 OK です。
以下の性質は、上記の厳密な定義から帰結されます。
- "0" が存在して、0 + a = a, 0 × a = 0 が成り立つ
- "1" が存在して、1 + a ≠ a, 1 × a = a が成り立つ
- e1, e2 ∈ S について
(e1 + e2) ∈ S かつ e1 + e2 が一通りに定まる
- e1, e2 ∈ S について
(e1 × e2) ∈ S かつ e1 × e2 が一通りに定まる
- 分配法則が成り立つ。 a, b, c を K の任意の元とするとき、a(b + c) = ab + ac, (a + b)c = ac + bc が成り立つ。
特に、 集合 S の元が有限個しかなく、S が体をなすとき、これを
有限体 と呼びます。
1 ビットの演算 GF(2)
上記の"+"と"×"が定義できるもっとも単純な集合(有限体)として、
0, 1 の二値しかない集合を考えます。
0, 1 という記号は仮に決めただけで、この集合の元は (a, b) でも、(甲、乙) でもかまいませんが、
ここでは 0,1 としておきます。
この 0, 1 に対し、以下のような「+」と「×」を定義してみます。
これは、実はさっきの「P で割った余りの演算」で、P=2 (2 で割った余り) の演算と同じです。
1 + 1 = 0 なのが目新しいですが、それ以外は普通の整数の演算と同じです。
特に+は bit 演算の xor に、×は bit 演算の and になっています。
こうすると、引き算、割り算(+余り) も定義できます。
足し算と全く同じになっています。普通の足し算、引き算に慣れると変に感じますが、特に問題はありません。
- 割り算、余り:
割られる数→
↓割る数 | 0 | 1 |
|---|
| 0 | - | - |
|---|
| 1 | 0 ... 0 | 1 ... 0 |
|---|
1 / 0 や 0 / 0 は定義できません。
(前者は 0 x ? = 1 となる ? は存在しないし、後者は 0 x ? = 0 を満たす ? は 0 でも 1 でもいい)
また、余りは発生しません。
なお、こうして作った演算は、GF(2) と呼ばれます。GF は Galois Field の略で、2 は元の数 (0, 1) をあらわしています。
ビット列の多項式表現
さて、先ほどは 0,1 の 2 つの元での演算 ( GF(2) )を定義しました。これを用いて、
先ほど説明した「普通の割り算に近いけど、繰り下がりが起こらないもの」という演算を定義してみます。
そのためには、まずビット表現の捕らえ方を変えてみます。
先ほどは、ビット表現を、とても大きな整数として見ていました。
"01" なら 1 ですし、"1001" なら 9 、"10010100" は 148, "1001111011111011010010110101" なら 166704309 という風に、一番右の桁を 1 の位、次の桁を 2 の位…という風に見ていました。
例として、ビット表現 1001 が数値の 9 になる仕組みを、以下に示します。
1 0 0 1 ----> 8 + 1 = 9
(8の桁) (4の桁) (2の桁) (1の桁)
これは、2 つ目の桁の "1" は、1 つ目の位の 2 倍だという前提で計算されていました。
これに対し、少し桁の結合方法を変えて、2 つ目の桁が 1 つ目の桁の 「x 倍」である、という風に考えてみます。
3つめの桁は x
2 倍になります。この方法で、1001 を表現すると
1 0 0 1 ----> (x^3 + 1)
(x^3 の桁) (x^2 の桁) (x の桁) (1の桁)
となり、 (x
3 + 1) となります。
(ただし、 x
n を x ^ n と書きました)
このようにすると、1001... というビット列は、x の多項式になります。また、その係数は必ず 0 か 1 になります。
元々の数値による表現がほしければ、x = 2 を代入すると、
(x^3 + 1) = 2 ^ 3 + 1 = 8 + 1 = 9
となり、元々の数値表現での値が得られます。
多項式上での演算
ビット列を多項式で表現できるようになりました。ここで、この多項式上で演算をすることを考えてみます。
ポイントは、x
2 + x + 1 のように、x を含んだ形で演算をすることです。
例えば、0, 1, x, x+1 の 4 つの元を持つ多項式の集合を考えてみます。
この集合を有限体とするような、+と×を探してみます。
- 足し算:
| + |
0 |
1 |
x |
x+1 |
| 0 |
0 |
1 |
x |
x+1 |
| 1 |
1 |
0 |
x+1 |
x |
| x |
x |
x+1 |
0 |
1 |
| x+1 |
x+1 |
x |
1 |
0 |
- かけ算:
| × |
0 |
1 |
x |
x+1 |
| 0 |
0 |
0 |
0 |
0 |
| 1 |
0 |
1 |
x |
x+1 |
| x |
0 |
x |
x2 |
x2+x |
| x+1 |
0 |
x+1 |
x2+x |
x2+1 |
足し算はとてもきれいにまとまりました。値は全て (0, 1, x, x+1) という元々の元に含まれています。
しかし、かけ算は元々の元 (0, 1, x, x+1) から外れてしまう値が出てきました。
これを、x
2 + x + 1 で割った余りで置き換えてみると、とてもきれいにまとまります。
- x2 = x + 1
- x2 + 1 = x
- x2 + x = 1
という関係が成り立つので、先ほどのかけ算の表は以下のように書き直すことができます。
| × |
0 |
1 |
x |
x+1 |
| 0 |
0 |
0 |
0 |
0 |
| 1 |
0 |
1 |
x |
x+1 |
| x |
0 |
x |
x+1 |
1 |
| x+1 |
0 |
x+1 |
1 |
x |
この (x
2 + x + 1) を生成多項式と呼びます。
これは、普通の CRC の計算で素数で割り算をしていたのと同じ意味を持ちます。
CRC の計算元は、割る数以下の、限られた値です
こうして構成できた演算は、以下の性質を持ちます。
- 元は 4 つ (22)
- x の係数は GF(2)の元
- 有限体の性質を満たす
これを、「GF(2) の 2 次の拡大体」や、「GF(2
2)」と呼びます。
GF(22) のべき表現
先ほどは、0, 1, x, x+1 の 4 つの元からなる拡大体を示しました。
この世界では、以下の性質が成り立っています。
- xi の係数は、GF(2) に従う
- 分配法則 (a + b) × c = a × c + b × c が成立する
- x2 + x + 1 = 0 が成立する
この世界で、x
i (x のべき乗) を考えてみます。
この集合は元は 4 つだけなので、x
i も 0, 1, x, x+1 のいずれかと等しいことになります。
計算方法としては、(x
2 + x + 1) で割ったあまりを計算します。
| x | = x |
|---|
| x2 | = (x2 + x + 1) + x + 1 = x + 1 |
|---|
| x3 | = (x2 + x + 1) (x + 1) + 1= 1 |
|---|
| x4 | = x3・x = x |
|---|
x
3 で 1 になっているので、このあと x
5, x
6, x
7... も繰り返します。
また、x
0 (= 1), x, x
2 に 0 を加えると、この集合のすべての元を網羅したことになります。
ここで、{x
i | 0 ≤ i < 3 } が GF(2
2) の 0 以外のすべての元を網羅しているのは、
偶然ではありません。
もし x
i = x
j ( 0 ≤ i < 3 , 0 ≤ i < j < 3)となる i, j が存在してしまったら、
両辺を x
i で割って、x
j - i = 1 が成り立ってしまいます。
そうすると、x = 1 または x
2 = 1 が成立することになりますが、これは
x
2 + x + 1 = 0 と矛盾してしまいます。
一方で、x
3 = 1 になったのも偶然ではありません。GF(2
2) には 4 つしか元がなく、
そのうち 1 つは 0 なので、x
i は周期 3 で繰り返すことになります。
GF(2) の n 次の拡大体: GF(2n)
先ほどは GF(2
2) の構成方法を書きました。
これは、0, 1, x, x+1 の 4 つの元を持つ多項式の集合でした。
これに対し、x の 2 次や 3 次の項を含ませると、もっとたくさんの元を持つ集合を考えることができます。
2 次の項を入れると、
{0, 1, x, x+1, x
2, x
2+1, x
2+x, x
2+x+1}
の 8 つの元を定義できます。
この元に対しては、最高次が x
3 となる生成多項式を探してみます。
生成多項式は既約多項式でないといけないので、(1 + x + x
3), (1 + x
2 + x
3) などが使えます。
(足し算、かけ算の表は大きくなるなので省きます)
このように、GF(2) に対して、n 次の拡大体を考えることができます。
これら拡大体は、以下のような、パソコンでの処理に都合のよい性質があります。
- 各桁を独立に足し算できる。引き算において繰り下がりがない。
- 任意の n に対して、2n 個の元を持つ集合に対する演算を定義できる
CRC の値は、ビット列をこの GF(2
n) にあてはめたときの値そのものです。
例えば CRC32 であれば、あるビット列を GF(2
32) の元に対応させたとき、
対応する多項式を計算します。その多項式を再度ビット列になおしたのが CRC の値です。
