大規模なシステムにはトラブルがつきものです。こうしたトラブルに対処する基本は、途中の計算結果のバックアップを取っておくことです。定期的にバックアップを取っておけば、トラブルの原因解析や計算をやり直す手間が省けます。
とはいえ、並列システムでは適当に保存しているだけでは余り役に立ちません。各プロセッサがばらばらに保存しても、各プロセッサのクロックはばらばらなのでどの状態とどの状態が対応しているのかが分かりません。また、プロセッサ間を移動しているメッセージがあった場合、このデータをどう扱うかも難しい問題です。条件分岐も繰り返しもなく、ひたすら進むプログラムなら、プログラムを書く段階で保存するポイントを指定することができますが、複雑な分岐を持つプログラムではそれも難しくなります。
ここでは、システム全体の様子を記録するのを目標として、理論的な考察を行います。流れは

Local State, Global State, Consistency, Cutなどの言葉を定義する
状態の記録における問題点を指摘する
Chandy-LamportのGlobal Stateを記録するアルゴリズムを示す

となります。なお、ここでも時刻は全てvector clockを用いています。

色んな言葉の定義

Local State, Global State

Local Stateとは、各プロセッサが持つ状態のことです。このLocal Stateを各プロセッサについて集めたものが Global Stateです。
あるGlobal StateがプロセッサPiのイベントeを含むとは、 Global StateがPiのLocal Stateを含み、かつそのLocal Stateが eの後に記録されたものであればいいです。

メッセージの状態

ここでは、メッセージの送受信のタイミングを問題にするので、これを表す記法を導入します。

time(x)イベントxが起きた時刻(Vector Clock)
send(m)…mを送るイベント
recv(m)…mを受信するイベント

ここで、あるメッセージについて、送信は必ず受信よりも先に起こります。なので、time(send(m)) < time(recv(m))が成立します。
また、メッセージの送信側と受信側の二つのプロセッサのLocal Stateを含むGlobal Stateについて、

send(m)を含み、recv(m)を含まない…Transit(送信中)
recv(m)を含み、send(m)を含まない…Inconsistent(不整合)
inconsistentなメッセージが無い…Consistent
transitなメッセージが無い…Transitless
transitlessで、かつconsistent…Strongly Trnasitless

と定義します。ここで注意するのは、transitlessな状態はinconsistentでも良い、ということです。単なる定義の問題ですが。

どういう風に役に立つか

状態を記録する場合、本当は全プロセッサについて実時間が等しいのが望ましいのですが、それはなかなか保証できません。しかし、inconsistentなメッセージが無ければ、 (Causal Ordering of eventsが保証されれば) もし同時に起こったとしても、おかしくありません。逆にinconsistentなメッセージがあれば、そのGlobal Stateは実時間上で同時には起こりえません。
また、transitなメッセージがあった場合は、プロセッサの状態を記録するだけでは情報が足りません。こういう時は、メッセージの送信路を監視するか、 Transitなメッセージが到着次第記録し、プロセッサの状態に合わせることで完全な状態を記録することができます。

Cutとして見る(参考)

実例を見てみる

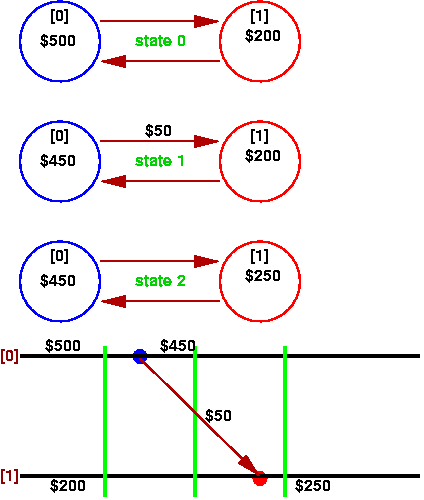
例えば、下図のようなシステムを考えます。 AとBは銀行の口座が何かで、お互いネットワークで情報をやりとりできます。 state0ではAは$500, Bは$200持っていますが、 state1でAはBに$50送金します。送金した$50は、state 2で到着します。このシステムを記録する時、起こり得るケースを考えてみます。

この場合、[0], [1]及び送信中のメッセージを記録して合計すれば、その値は常に$700で一定であるべきです。例えば、

state 0 の[0], state 0 のメッセージ, state 0 の[1](Stlongly Transitless)
state 1 の[0], メッセージ, [1](Consistent)
state 2 の[0], メッセージ, [1](Stlongly Transitless)

のそれぞれを合わせたGlobal Stateを考えれば、これらの合計はちゃんと $700になります。
しかし、以下のような組み合わせでは、合計が$700になりません。

state 0 の[0], State 1 のメッセージ, State2の[1](inconsistent)
state 2 の[0], Stete 1 のメッセージ, State0の[1](transit)

このように、ちゃんと合計を求めるためには、送信中のメッセージもカウントできる場合はConsistent、できない場合はStrolgly Consistentである必要があることが分かります。この例でも分かるように、Global Stateの中でもConsistentなもの以外は扱いにくく、記録する場合はConsistentな状態を記録したい、ことが分かります。

Chandy-LamportのGlobal Stateを記録するアルゴリズムを示す

このアルゴリズムは、Global Stateを簡単に記録するものです。 ConsistentなGlobal stateを記録する、例えばシステム中のある値の合計を求める、といったよく使われる操作のために一々全てのメッセージについてstrolgly transitlessであることを示すのは大変です。このため、Global Stateの理論的裏付けを持たせつつ、簡単に合計を求められる方法として、Chandy-Lamportのアルゴリズムを説明します。

定義

このアルゴリズムでは、マーカーという特別なメッセージを用います。なお、このシステムでは送信したメッセージは送った順に到着し、送ったメッセージが途中で失われることはないものとします。また、送信路は全プロセス間にあるものとします。

各プロセスはあるポイントに入ると、現在の状態を記録する。
これは一台のプロセスだけが記録をしてもいいし、勝手に複数のプロセスが記録をしてもよい
状態を記録したプロセッサは、全ての送信路に"マーカー"という特殊なメッセージを送る。これは、次のメッセージより先に送らなくてはならない
マーカーを受け取ったプロセッサは、まだ自分が状態を記録していなければ、 "Empty Sequence"として現在の状態を記録する。記録した後は、先のルールに従う
もしマーカーを受け取ったプロセッサが既に現在の状態を記録していれば、記録した時からマーカーを受け取った時までのメッセージを記録する。

ポイントは、記録の引き金としてダミーのメッセージであるマーカーを送信し、 Inconsistentな状態を防いでいることです。また、記録後に到着したメッセージを追加で記録することで transitなメッセージをちゃんと数え漏れないようにしています。

実例

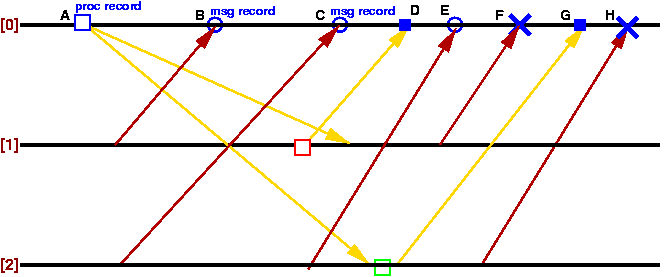
これも実例を挙げてみます。 □がプロセス状態の記録を、○がメッセージの記録を、■がマーカーの到着を、 ×がメッセージが記録されなかったことを示します。なお、プロセス[0]以外のマーカーやメッセージの記録は省いてあります。

[0]はAでプロセスの状態を記録し、マーカーを[1]と[2]に送信します。このとき、[1]はもう記録済みですが、[2]は自分の状態をまだ記録していないので、マーカー到着後すぐに状態を記録し、マーカーを返信してきます。 (実際には[1]から[2]、[2]から[1]へもマーカーが送信されます)
プロセッサ[0]では、自分の状態を記録(A)してから [1]からのマーカーが来るまでに到着した、 [1]からのメッセージを記録(B)し、また[2]からのメッセージが来るまでに到着した[2]からのメッセージを記録(C,E)します。 FやHは、もうマーカーを受け取っているので、メッセージは記録されません。

並列分散システムを記録する