[an error occurred while processing this directive]
[an error occurred while processing this directive]
並列分散システムでの「クロック」
クロックといっても、ここでいうのは何秒とか何分とかいうものではなく、
プログラムの進度を表す指標みたいなものです。
このクロックは並列システムにおいてプログラムが進んだ道筋を
各プログラムの立場で把握するもので、障害復旧などに役立ちます。
ここでの説明は、
- まずここで述べるクロックの概要を説明する
- このクロックを定義に忠実に表わしたVector Timeを示す
- Vector Clockを簡易にしたLamport Timeを示す
という順番で進めていきます。
ここで考えるクロックについて
「順序関係」「因果関係」を表すのがクロック
ここで述べるクロックの基本は、二つのイベントについて、どちらが先に起こったかわかる
というものです。例えば、以下のような順でイベントが起こったとします。
[0]----A--------B--C---
以下、このような線を一定の時間軸、[0]をプロセッサ番号、(n)をクロックとします。
また、軸上のA,B,Cはイベント、tAなどはその時間を表す記号とします。
上のようなシステムで、例えばA-Bの時間はB-Cの時間より長いですが、それは
ここでは問題にしません。
一方で、Bという地点はAの結果を知ることができるため、
t
A < t
Bであると考えます。
同様にt
B < t
Cから、
t
A < t
B < t
Cとなります。
必要とされるのはこの順序(因果)関係だけになります。
因果関係というのはここではややミスマッチな言葉です。
ひょっとしたら、AでもBでも状態は変化せず、
Bの結果の原因がAにある…とは言えないかもしれません。
しかし、ここでは「プログラムによってはBはAの結果を知り得る」ということで
「因果関係」と呼ぶことにします。
独立したプロセスの場合
先に、順序関係のみを問題にすると言いましたが、この場合はどうでしょうか?
[0]--A--------
[1]--------B-
[0]と[1]は全く関係なく動いているプロセスで、共通のクロックやメモリは持たず、
情報をやりとりするにはメッセージを送り合うしかないものとします。
このとき、上の図ではAの情報はBに伝わっていませんし、逆もありません。
実時間ではAがBより先に起こっているのですが、BはAの結果を見ることはできないので、
AとBに「因果関係」はありません。
よって、AとBは比較しても無意味だと考えます。
繰り返しになりますが、これは決め事で、後々便利なのでここでは意味がないと考えるというものです。
このようなAとBの関係を"Concurrnt State"と言い、記号||で表します。
この「比較が無意味」ということについて、もう少し考えてみます。
もしもし[0]と[1]の二つのプロセスがクロックを共有しているなら、AとBは比較可能になります。
あるいは、二つのプロセスが共通のメモリを持っていて、随時ここを参照しているなら、
BはAの結果を利用することができます。そうすると、
t
A < t
B
という関係が成立します。
しかし、実際には[0]と[1]では共通の時間の基準を持たないため、[0]や[1]というプロセスの
立場にとってみると、AとBの比較は無意味であることが分かると思います。
メッセージ
以下のような並列システムでは、どのように考えればいいでしょうか。
[0]---A-----B--C--
/
/
/
[1]--D--E----F----
これは、Eで何らかのメッセージが送信され、Bでそれを受け取ったことを示しています。
E,Bはそれぞれ「送受信した直後」の状態とします。
まず、明らかに定義として
tA < tB < tC、
tD < tE < tF
の関係があります。また、メッセージの授受が行われていますが、
これについて、
tE < tB
と定義します。
さて、残りの関係はどうでしょうか?
先と同様、確かに実時間ではAはDより後ですが、この比較は意味を持ちません。
よって、クロックが満たすべき条件は先の式だけになります。
まとめ
ここで言うクロックは、以下の二つの原理に基づいています。
- 同一プロセッサで、AがBより(実時間で)先に起こった場合、tA < tB
- メッセージの送信Sと受信Rについて、tS < tR
>
これは、イメージ的に言うと
「t
A < t
B」のとき「BはAの情報を見ることが出来る」
となります。
すると、二つの時間t
Aとt
Bの関係は、以下の四つがあります。
- tA = tB
- tA < tB
- tA > tB
- tA ||tB (tAとtBは比較不能, concurrent)
(この他にも、=と<のorを取って<=、同様に>=や!=(not equal)も定義できます)
このように任意の二つの項についての関係が「=, >, <, ||」の四つで表せるものを
半順序関係といいます。
これは普通のスカラーだけでは、「比較不能」という状態が作れないのでうまく表わせません。
(スカラーは二つの数について一意に順序が決定できる全順序関係を持つため)
このため、後の方でVector Timeが導入されることになります。
Vector Time …ちゃんと半順序を表す
では、本命のVectorat Clockです。
ベクトルというのは、クロックを一つの数字ではなく、プロセッサの数だけ並べて「ベクトル」とするという意味です。
よって、三つのプロセッサがあればクロックは全て三次元ベクトル、四つあれば四次元ベクトルで表します。
このベクトルを、各プロセッサが「別々に」持っていて、メッセージにもこのVector Clockが添付されます。
ベクトルの中身ですが、感覚的には各要素が各プロセッサのクロックを表しています。
以下、プロセッサを0,1,2、それぞれのプロセッサが持つVector ClockをC
0,C
1,C
2、
C
iのVector Clockの要素をC
i[0],C
i[1],C
i[2]とします。
また、二つのベクトルV1, V2の比較を定義します。
V1とV2の対応する要素について、全ての要素についてV1の方がV2より大きいとき、V1 > V2であるとします。
また、逆にV1 > V2という関係があるなら、対応する全ての要素についてV1の方がV2より大きいとします。
例えば、以下のような関係が成り立ちます。けっこう感覚的で分かりやすいのでは?
- (1, 2) = (1, 2)
- (1, 2) < (2, 3)
- (1, 2) || (2, 1)
このとき、Vector Clockは以下のルールに従うものとします。
- 初期値はプロセッサによって異なる
- メッセージのやりとりが無いときは、クロックは変化しない
- iがjにメッセージを送信するときは、送信直前のクロックを添付して送り、
送信後Ci[i]を増加させる
- jがiからのメッセージを受信したら、メッセージのクロックと受信直前のクロックを比較し、
大きい方より大きい値を次のクロックとする
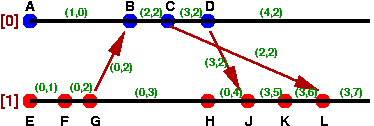
では、実例を示します。
この図で、(a, b)のように示されているのがVector Clockです。
矢印の近くにあるのは、メッセージに添付されたクロックです、
まずプロセッサ[1]ですが、E->F->Gは時間の推移に従って後の成分が1ずつ増えます。
Gでメッセージを送信するわけですが、このときFのクロック(0,2)を
添付して送ります。そして、[1]自体のクロックはGでも1増えて(0,3)になります。
さて、このメッセージを受信したBでは、Aのクロック(1,0)とGからのメッセージに
付いてきたクロック(0,2)を比較します。そして、先のルールに従い、前の成分は
Aから取り1、後の成分はGから取り2となります。さらに、前の成分に
1を加え、次のクロック(2,2)とします。
C, Dではメッセージの送信がありますが、これもGと同様、送信する直前のクロックを
送ります。そして、Dからのクロックを受けるJでは直前のクロック(0,4)とメッセージの(3,2)
を比較し、前の成分は3、後の成分は4に1を加え(3,5)となります。
同様に、Lでは直前の(3,6)とメッセージの(2,2)を比較し、後者に1を足して(3,7)とします。
こうして計算したVector Clockを用いると、二つのイベントの時間的関係を
決定することができます。
地点AとBについて、Vector Clockの値がV
A及びV
Bであるとき、
以下のような関係が成り立ちます。
| VA < VB |
BはAより先に起こった |
| VA > VB |
AはBより先に起こった |
| VA = VB |
AとBは同じプロセッサで同時に起こった |
| VA || VB |
Concurrent State、異なるプロセッサで比較不能な時刻に起こった |
例えば上の図でBとHは(2,2)||(0,4)よりconcurrent、
CとKは(3,2)と(3,5)でKが後、などが分かります。
Vector Clockのお手軽版…Lamport Clock
先に述べたように、ここでの「クロック」はスカラーでは完全には表せません。
しかし、この「比較不能」なものにも勝手に順番を決めてよいとすると、
次のような比較的簡単な仕組みで計算することができます。
- メッセージのやりとりが無いとき、クロックはイベントの発生に従って単調増加する
- メッセージを送信するときは、送信直前のクロックを添付して送り、その後クロックを増加させる
- メッセージを受信したら、メッセージのクロックと受信直前のクロックを比較し、
大きい方より大きい値を次のクロックとする
なお初期値やクロックの増加数は自由ですが、以下の例では
初期値は0、増加数は1としています。
先のVector Clockと比較すると、ベクトルの成分を区別せず、
全て同じ成分を比較したり増加させたりしたのに対応します。
地点AとBについて、Lamport Clockの値がLC
A及びLC
B、
Vector Clockの値がV
A及びV
Bであるとき、
以下のような関係が成り立ちます。
| LCA < LC2 |
VA < VB又はVA || VB |
AがBより先に起こっていることはない |
| LCA > LC2 |
VA < VB又はVA || VB |
BがAより先に起こっていることはない |
| LCA = LCB |
VA = VB又はtA || tB |
AとBは同時に起こっているか、比較不能 |
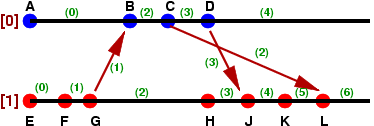
これについて、以下の例で実際にLamport Clockを計算してみます。
まずプロセッサ[1]ですが、E->F->Gは時間の推移に従って1ずつ増えます。
Gでメッセージを送信するわけですが、このときGの直前のクロック(1)を
添付して送ります。そして、[0]自体のクロックはGでも1増えて(2)になります。
さて、このメッセージを受信したBでは、直前のクロック(0)とメッセージに付いてきた
クロック(1)を比較します。そして、大きい方に1を加え、次のクロック(2)とします。
C, Dではメッセージの送信がありますが、これもGと同様、送信する直前のクロックを
送ります。そして、Dからのクロックを受けるJでは直前のクロック(3)とメッセージの(3)
を比較し、大きい方(この場合は同じなので3)に1を加え、新しいクロックとします。
同様に、Lでは直前の(5)とメッセージの(2)を比較し、大きい方の(5)に1を加え(6)とします。
このLamport Clockは実装が簡単な反面、数字だけ見ると
比較できない部分まで比較できてしまいます。
例えば上の図だと、BとH,CとHは本来「比較不能」となるべきですが、
見かけ上B < C = Hのように見えます。
しかし、メッセージの到着が送信に先行しないようにする、といった
実用的な用途ではLamport Clockで十分なことも多いようです。