[an error occurred while processing this directive]
[an error occurred while processing this directive]
Causal Ordering of Messages (メッセージの到着を送信順に整列させる)
Causalとは直訳すると「因果関係の」、Causal Orderingは「因果関係の順番」です。
これは、並列システムがどういう動作をしているのかを把握したり、
状態を記録する際に大事になってくる概念です。
普通に設計したシステムはCausal Orderingを満たしていないことが多いですが、
これを満たすようにシステムを制限することで、システムの動作や
アルゴリズムの見通しが良くなります。
ここでの説明は、
- メッセージ同士が順番抜かしをしない「Causal Ordering of messages」を定義する
- メッセージが一度に全てのプロセッサに送信される(Broadcast)場合に用いられる
Birman-Schiper-stephenson Protocolという実現法を示す
- 1:1のやりとりでも用いることができるSchiper-Eggli-sandoz protocolという実現法を示す
という順で進めていきます。
☆なお、ここで言う時間は全てVector Timeとします。
Causal Ordering of messagesとは
まずは定義
Causal Orderingは「因果関係の順番」となりますが、
まずよく出てくるのはCausal Ordering of eventです。
これはCosistency(一貫性)とも言われ、状態の記録では非常に大事になります。
この意味は、因果関係がちゃんとした順で起こるということで、
「同一プロセッサの中で、実時間でイベントAよりBが先に起こった場合、
clockA < clockBが成立する」
及び
「あるメッセージを送った時点Sと、それが受信された時点Rについて、
clockS < clockRが成立する」
ということです。
これらはここで考えるクロックの性質そのものです。
さて、ここで問題にするのはCausal Ordering of messagesです。
これは一つのメッセージの送信受信の関係ではなく、
二つ以上のメッセージについての関係を考えます。
メッセージm1とm2について、m1の送信時刻をtm1s、受信をtm1r、
同様にm2の送受信をtm2s, tm2rとするとき、
「tm1s < tm2s なら
(tm1r < tm2r 又は tm1r || tm2r )」
かつ
「tm1r < tm2r なら
(tm1s < tm2s 又は tm1s || tm2s )」
が成り立つなら、Causal Oredering of messagesが成立していると考えます。
簡単に言うと、「Vector Clock的に先に送信したメッセージが後に着くことはない」
ということです。
具体例
具体例を見てみます。
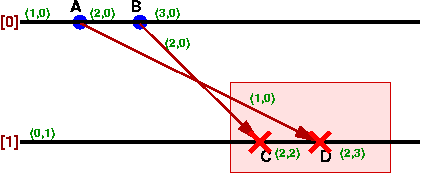
メッセージの送信・受信を調べてみると、
- (1,0)A-D(2,3)
- (3,0)B-C(1,1)
となっていて、
送信の時はt
A < t
Bなのに、受信の時はt
D > t
C
と順番が逆転しています。
つまり、メッセージA-DとB-Cとの間でCausal Orderingが乱れています。
この場合は送信と受信が同じメッセージの間で追い抜きが起こっているので、
比較的容易に分かります。
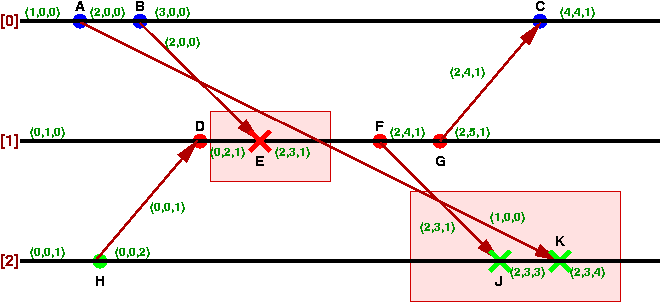
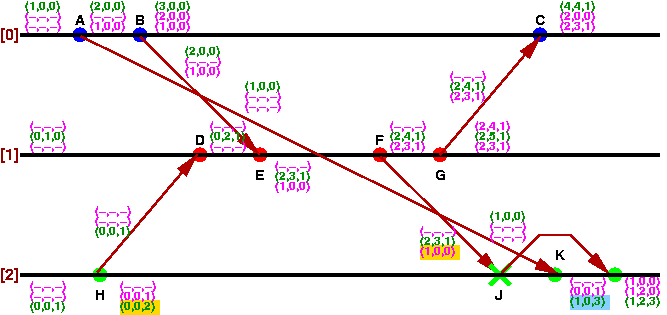
次はもう少し複雑な例を示します
この場合も各メッセージを調べてみます。
- A(1,0,0)-K(2,3,4)
- B(2,0,0)-E(2,3,1)
- F(2,3,1)-J(2,3,3)
- G(2,4,1)-C(4,4,1)
- H(0,0,1)-D(0,2,1)
この場合は送信と受信を共に同じにするメッセージはありません。
しかし、Vector Clockを比較するとB-EとA-K、F-J,とA-Kの間で
Causal Orderingが崩れていることが分かります。
どうすればCausal Orderingを維持できるのか
では、どうすればこのCausal Orderingを維持できるのかを
考えてみます。
…といっても原理は大したことはなくて、速く到着しすぎたメッセージを
退避させ、新しいメッセージを受信した後、早く付いたメッセージを
受信するか判断し、良ければ受信する、というものです。
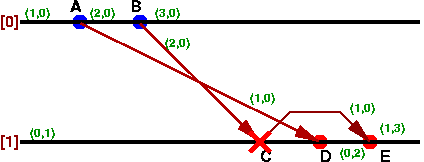
先の例だとこうなります。
上のXが付いた所で何らかの判断をして、メッセージの到着を止めておきます。
そして、A->Dのメッセージが着いた後で、これを受信すればよいのです。
とはいえ、どのような場合に退避が必要なのかは今までのVector Clockを
見るだけでは分かりません。そこで、その他のメッセージを用いた
プロトコルが考案されています。これを順に述べていきます。
Birman-Schiper-Stephenson Protocol
このアルゴリズムは、メッセージが全てbroadcast(あるプロセッサから
全プロセッサへの送信)の場合に用いることができます。
Vector Clockを少し変えることでそのメッセージを受信してもいいか、分かるようになっています。
アルゴリズムの説明
用いるのはVector Clockと同様、プロセッサ数個の要素を持つベクトルです。
メッセージにクロックを添付するのも同じです。
ただし、値の増加のさせ方が少し異なります。
☆以降、メッセージを送信するプロセッサをPi、受信するプロセッサをPjとします。
- クロックの初期値は(0,0,...,0)
- プロセッサは、メッセージの送信時以外のイベントではクロックを増加させない。
- Piがメッセージを送信する時は、まずPiのクロックのi番目成分VCPi[i]を
1増加させる。このi番目成分は、Piが送信したメッセージ数を表わす
- メッセージを送信する時は、まず上に従ってクロックを増やす。その後、増加させた
クロックを添付して送信する
- メッセージがプロセッサPjに届いたら、Pjは自分のクロックVCPjと
メッセージに添付されたクロックVCmについて、以下の条件を共に満たせばメッセージを
受信する。満たさなければ、受信待ちの列に入れる。
- VCPj[i] = VCm[i] - 1
- iと異なる全てのkについて、VCPj[k] >= VCm[k]
受信待ちの列では、メッセージはVector Timeの順にソートしておく。
Concurrent(||、 比較不能)なものは到着順でよい
- メッセージを受信した場合は、もしVCMの要素でVCPj
より大きいものがあればそれで上書きする
- メッセージを受信してクロックが更新された場合、受信待ちの列から受信出来るものを
順に受信する
决まりだけ書くとややこしそうですが、要は自分より前に送信されたメッセージが
全て受信されるまで受信を延期するわけです。その条件が上に挙げたものです。
適応例
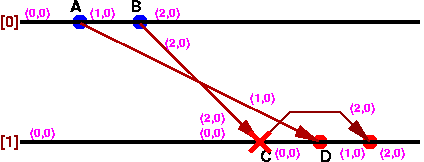
ともあれ、例を見れば分かってもらえると思います。
先程と同じ図ですが、ピンク色で書かれているのはVector Clockではなく、
BSSのクロック(?)です。
ポイントはメッセージを送信する*前に*クロックが上がること、
メッセージの送信でのみクロックが増加すること、
Cではメッセージのクロックが(2,0)に対しプロセッサ[1]のクロックが
(0,0)なので、上の条件に違反し受信が延期されていることです。
Schiper-Eggli-Sandoz Protocol
上に述べたBSSプロトコルは単純ですが、全てのメッセージがbroadcastでないと
使えないという致命的な欠点があります。
この解決としては、1:1のメッセージ送信についても、元々メッセージが送信されて
いなかったプロセッに対しダミーのメッセージを送信する、なども考えられますが、
メッセージの送信自体を増やすのはあまり好ましくありません。
これに対し、ここに述べるSchiper-Eggli-Sandoz Protocolは少し複雑ですが、
あらゆるメッセージ送信に対し使えます。
アルゴリズムの説明
このプロトコルでは、各プロセッサはVector Clockと共に、自分以外のプロセッサの数だけ
Vector Clockを格納できる配列を持っています。
プロセッサiは自分のVector Clockであるt
Piの他に、Vector Clockの配列
V_Piを持っています。
プロセッサ数がn個、それぞれをP0,P1, .. ,Pi, .., P(n-1)と呼ぶと、各プロセッサが
V_Piという配列を持っていまて、V_Piの要素はV_Pi[0],V_Pi[1],...V_Pi[n-1]まで、
ただしV_Pi[i]はありません。これらの要素にはVector Clockが入り、初めは空です。
以降、この配列をどう用いるかを述べていきます。
なお、メッセージを送信するプロセッサをi、受信するプロセッサをjとします。
- tPiは通常のVector Clockで、メッセージの授受により更新される
- メッセージmを送信する時は、送信直前のクロックtPiとV_Piを
添付する。これを。tMとV_Mと呼ぶ
- メッセージを送信後、送信した時のtPiをV_Pi[j]に格納する。
空の場合はそのまま、もうデータが入っているときも上書きする。
その後、tPiを増加させる
- メッセージがPjに到着した時、tM・V_MとtPj・V_Pjについて
以下の条件に従って受信するかどうかを决める。
- もしV_M[j]が空なら、メッセージを受信する
- V_M[j]にもう値がある場合、その値のクロックがtPjより古ければ(V_M[j] < tPj)
メッセージを受信する。
- その他の場合(V_M[j] || tPj又はV_M[j] > tPj)は受信しない
受信しない時は、受信待ちの列に入れる。
- 受信した場合は以下のルールに従ってクロックを更新する
- V_MにあってV_Pjには無い列があれば、その列をV_Mの値でV_Pjを更新する
(但し、j番目の列はV_Pjに無いので除く)
- V_MにもV_Pjにもある列は、二つのVector Clockの値をマージする
その上で、受信できるメッセージがあれば受信する
…文字で書くとややこしいですが、要はメッセージのVector Clockが
V_Pj[i]より古ければメッセージを受信し、配列をマージし、
条件を満たす受信待ちメッセージがあれば受信するわけです。
適応例
想像できるように、このプロトコルではたくさんの数字が出てきて
人力でシミュレーションするのはけっこう大変でした。
ピンク色のものがSESの配列の要素、緑色はVector Clockです。
SESの配列は自分に当たる要素が抜けているので、ここに
Vector Clockを入れたような格好ですが、更新する手順は全く異なります。
(-,-,-)となっているのは、SESの配列が空であることを示しています。
こちらは複雑なので順を追って見てみます。
まず、緑のVector Clockは先程と同様に変化します。JでXが付いているところは
メッセージの受信が延期されているので、クロックは変化しません。
まずAですが、メッセージが送信され、その後上から3番目の段に
メッセージに添付されたクロック、(1,0,0)が格納されています。
なお、送信されたメッセージに、このピンク色の(1,0,0)は無いのが
ポイントです。
次のBで送信されたメッセージには、三段目に(1,0,0)が付いています。
Eでの到着では、Bからのメッセージに[1]に当たるクロックが含まれていないので
そのまま受信されます。その後、ピンク色のSES配列がマージされます。
ここで、緑のVector ClockがピンクのSES配列にマージされたりはしないので、
注意して下さい。
最後に、Causal Ordering of messasgesのチェックが働く場合です。
Jでは、メッセージが[2]の成分(上から三段目)を含み、かつ
その値(1,0,0)がJ直前のクロック(0,0,2)とConcurrentで
「古くはない」ため、メッセージの到着は延期されます。
KでAからのメッセージが到着すると、
メッセージの値(1,0,0)とKのクロック(1,0,3)の比較になり、
(1,0,0) < (1,0,3)より受信が行えるようになります。